この記事はCAMPHOR- Advent Calendar 2017の21日目の記事です.
12月といえば,万人受けしなさそうなネタでブログを書いては「はてブが付かねえ」と文句を言う季節だが,今年もそういう方針で,TypeScriptでの型レヴェル計算について書く.型レヴェルでの自然数などが定義できると,リストに型レヴェルで長さを付けることができて,空リストの先頭の要素を取ろうとしてランタイムで落ちる,という悲劇が生じる可能性をコンパイル時に排除できてとても嬉しい*1.
なお,使用しているTypeScriptのヴァージョンは,少し古くて2.4.1である.これは,手元でたまたま2.6系のプロジェクトと2.4系のプロジェクトがあったのだが,2.6系だと型推論が停止しない(tscが"Maximum call stack size exceeded"で死ぬ)ことに気付き,悲しい気持ちになったからである.
型レヴェル真偽値#
あると色々便利なので,まずは真偽値を作る.
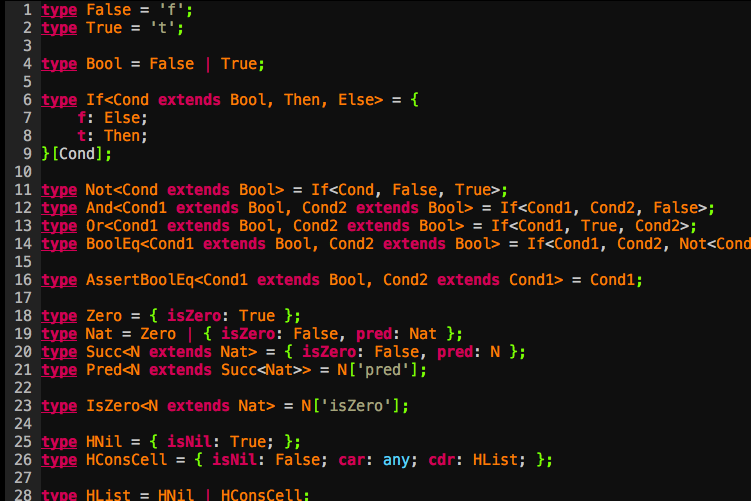
type False = 'f';
type True = 't';
type Bool = False | True;
ここではstring literal typeを用いて,False型とTrue型を定義している.Falseは値として文字列の'f'のみを,Trueは文字列の't'のみを取る型で,Boolはこれらのunion typeになっている.string literal typeのエイリアスとして定義している理由は直後に述べる.これを用いると,以下のような型レヴェルの条件分岐や論理演算を記述することができる.
type If<Cond extends Bool, Then, Else> = {
f: Else;
t: Then;
}[Cond];
Ifの定義を見てみよう.Ifは3つのgeneric parameterを取る型で,CondはBool(= 't' | 'f')の部分型であり,残りのThenとElseは任意の型になっている.{ f: Else; t: Then; }の部分はオブジェクトの型定義で,fというプロパティにElse型を,tというプロパティにThen型を持つオブジェクトを表している.最後の[Cond]はindex typeで,先に定義したオブジェクトのある(fまたはt)プロパティに含まれる型を取り出している.先程の種明かしになるが,このような操作をするために,Boolの定義にstring literal typeを用いたのだった.この例からわかるように,index typeを使えば,取りうる引数がstringの部分型に限られてしまうものの,型レヴェル関数がいとも簡単に記述できてしまう.
Ifを使った論理演算を幾つか記述してみよう.
type Not<Cond extends Bool> = If<Cond, False, True>;
type And<Cond1 extends Bool, Cond2 extends Bool> = If<Cond1, Cond2, False>;
type Or<Cond1 extends Bool, Cond2 extends Bool> = If<Cond1, True, Cond2>;
type BoolEq<Cond1 extends Bool, Cond2 extends Bool> = If<Cond1, Cond2, Not<Cond2>>;
let a: Not<True>;
// let a: "f"
let b: And<True, False>;
// let b: "f"
let c: Or<True, Not<True>>;
// let c: "t"
let d: BoolEq<True, False>;
// let d: "f"
また,異なるデザイン・チョイスとして,以下のように部分型関係を用いて事前条件を記述すれば,条件にそぐわない型がそもそも存在し得ないようにすることも可能だろう.
type AssertBoolEq<Cond1 extends Bool, Cond2 extends Cond1> = Cond1;
let a: AssertBoolEq<True, False>;
// error, Type '"f"' does not satisfy the constraint '"t"'.
型レヴェル自然数#
次に型レヴェル自然数を定義する.
type Zero = { isZero: True };
type Nat = Zero | { isZero: False; pred: Nat };
type Succ<N extends Nat> = { isZero: False; pred: N };
type Pred<N extends Succ<Nat>> = N['pred'];
type IsZero<N extends Nat> = N['isZero'];
ここでは,Zero型を「isZeroプロパティにTrue型の値を持つオブジェクト」として,Nat型を「isZeroプロパティにFalse型の値を持ちかつPredプロパティにNat型の値を持つ型と,Zero型との和」として定義している.Succ,PredおよびIsZeroの定義は見ての通りであるが,Predについての解説をしておくと,Zeroの前者は存在しないので,<N extends Succ<Nat>>とすることで,Pred<Zero>なる型が存在できないように制限をかけている.
以上で自然数の構成を与えることができた.便利のため,自然数のうち最初の幾つかに別名を付けておく.
type _0 = Zero;
type _1 = Succ<_0>;
type _2 = Succ<_1>;
type _3 = Succ<_2>;
type _4 = Succ<_3>;
type _5 = Succ<_4>;
type _6 = Succ<_5>;
type _7 = Succ<_6>;
type _8 = Succ<_7>;
type _9 = Succ<_8>;
再帰的な型定義#
Natの定義の際にしれっと再帰をしていた(type Nat = Zero | { isZero: False, pred: Nat };)のだけれど,再帰的な型定義を行いたい場合,自分自身の型名を参照するのは,オブジェクト型の中で行わなければならない.つまり,以下のような型定義はできない.
type Upto<N extends Nat> = If<IsZero<N>, Zero, N | Upto<Pred<Nat>>>;
// error, Type alias 'Upto' circularly references itself.
これは,以下のようにオブジェクト型とindex typeを用いて書かなければいけない.
type Upto<N extends Nat> = {
f: N | Upto<Pred<N>>;
t: Zero;
}[IsZero<N>];
let x: Upto<Three>;
// let x: Zero | Succ<Zero> | Succ<Succ<Zero>> | Succ<Succ<Succ<Zero>>>
オブジェクト型の中で再帰的に名前を用いた場合,名前の循環参照性がチェックされないらしく,上手くいく*2.
再帰的な型定義が書けるようになったので,2つの自然数を受け取って,一方が他方以下であるかを判定するLteq<M extends Nat, N extends Nat>型を定義する.
type Lteq<M extends Nat, N extends Nat> = {
f: If<IsZero<N>, False, Lteq<Pred<M>, Pred<N>>>; // Mが正でNが0ならFalse,それ以外なら双方の前者同士を比較
t: IsZero<N>; // MもNも0ならばTrue
}[IsZero<M>];
反対称律より,与えられた2つの自然数が等しいかどうかを返すNatEq<M extends Nat, N extends Nat>は次のように定義できる.
type NatEq<M extends Nat, N extends Nat> = And<Lteq<M, N>, Lteq<N, M>>;
// M ≤ NかつN ≤ MならばM = N
2つの自然数を受け取ってその和を返すAdd<M extends Nat, N extends Nat>型を定義してみる.
type Add<M extends Nat, N extends Nat> = {
f: Succ<Add<M, Pred<N>>>; // m + n = (m + (n - 1)) + 1
t: M; // 基底部; m + 0 = m
}[IsZero<N>];
let a: Add<_0, _1>;
// let a: Succ<Zero>
let b: Add<_2, _0>;
// let b: Succ<Succ<Zero>>
let c: Add<_5, _3>;
// let c: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>
let d: Add<_6, _8>;
// let d: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>>
加算が書けると,フィボナッチ数が書ける.
type Fib<N extends Nat> = {
f: If<NatEq<_1, N>, _1, Add<Fib<Pred<N>>, Fib<Pred<Pred<N>>>>>; // fib(1) = 1, fib(n) = fib(n - 1) + fib(n - 2)
t: Zero; // 基底部; fib(0) = 0
}[IsZero<N>];
let fib7: Fib<_7>; // let fib7: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>
乗算も書ける.
type Mul<M extends Nat, N extends Nat> = {
f: Add<M, Mul<M, Pred<N>>>; // m * n = m + m * (n - 1)
t: Zero; // 基底部; m * 0 = 0
}[IsZero<N>];
let a: Mul<_0, _1>;
// let a: Zero
let b: Mul<_2, _0>;
// let b: Zero
let c: Mul<_5, _1>;
// let c: Succ<Succ<Succ<Succ<Succ<Zero>>>>>
let d: Mul<_1, _8>;
// let d: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>
let e: Mul<_2, _4>;
// let e: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>
let f: Mul<_3, _6>;
// let f: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>>>>>>
乗算が書けると,階乗も書ける.
type Fact<N extends Nat> = {
f: Mul<N, Fact<Pred<N>>>; // n * fact(n - 1)
t: _1; // 基底部; 0または1のとき 1
}[Or<IsZero<N>, NatEq<_1, N>>];
let fact4: Fact<_4>;
// let fact4: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>>>>>>>>>>>>
let fact5: Fact<_5>;
// error, Generic type instantiation is excessively deep and possibly infinite.
少し話が戻るが,Upto<N extends Nat>型を使えば,自然数同士の引き算が安全に記述できる.
type Sub<M extends Nat, N extends Upto<M>> = {
f: Sub<Prev<M>, Prev<N>>;
t: M;
}[IsZero<N>];
let a: Sub<_4, _0>;
// let a: Succ<Succ<Succ<Succ<Zero>>>>
let b: Sub<_3, _2>;
// let b: Succ<Zero>
let c: Sub<_2, _5>;
// error, Type 'Succ<Succ<Succ<Succ<Succ<Zero>>>>>' does not satisfy the constraint 'Zero | Succ<Zero> | Succ<Succ<Zero>>'. Type 'Succ<Succ<Succ<Succ<Succ<Zero>>>>>' is not assignable to type 'Succ<Zero>'. Types of property 'pred' are incompatible. Type 'Succ<Succ<Succ<Succ<Zero>>>>' is not assignable to type 'Zero'. Types of property 'isZero' are incompatible. Type '"f"' is not assignable to type '"t"'.
型レヴェルリスト#
複数の型をまとめて扱えると楽しいので,型レヴェルヘテロリストを作る.
type HNil = { isNil: True };
type HConsCell = { isNil: False; car: any; cdr: HList };
type HList = HNil | HConsCell;
リストに入れることのできる型をカインドで制限したりしたくなると思うが,流石に無理そうな気がしたので諦めた.
取り扱いを簡単にするため,以下の型を用意する.
type HCons<Car, Cdr extends HList> = { isNil: False; car: Car; cdr: Cdr };
type Car<Xs extends HConsCell> = Xs['car'];
type Cdr<Xs extends HConsCell> = Xs['cdr'];
type Null<Xs extends HList> = Xs['isNil'];
type HSingleton<T> = HCons<T, HNil>;
手始めに,リストを逆順にするReverse<Xs extends HList>型を定義してみよう.実装はHaskellのbaseモジュールを参考にした.
type Reverse<Xs extends HList> = Rev<Xs, HNil>;
type Rev<Xs extends HList, T> = {
f: Rev<Cdr<Xs>, HCons<Car<Xs>, T>>;
t: T;
}[Null<Xs>];
type Upto3 = HCons<_0, HCons<_1, HCons<_2, HCons<_3, HNil>>>>;
let xs: Reverse<Upto3>; // let xs: HCons<Succ<Succ<Succ<Zero>>>, HCons<Succ<Succ<Zero>>, HCons<Succ<Zero>, HCons<Zero, HNil>>>>
次に,与えられた型レヴェルリストの長さを型レヴェル自然数で返すLength<Xs extends HList>を定義する.
type Length<Xs extends HList> = {
f: Succ<Length<Cdr<Xs>>>; // 1 + length(cdr(xs))
t: _0; // 基底部; 空リストの場合は0
}[Null<Xs>];
type Upto3 = HCons<_0, HCons<_1, HCons<_2, HCons<_3, HNil>>>>;
type LengthOfUpto3 = Length<Upto3>;
let len: LengthOfUpto3; // let len: Succ<Succ<Succ<Succ<Zero>>>>
HConsをたくさん書くのが大変なので,適当なリストを簡単に生成できるようにしたい.与えられた自然数Nに対し,0番目からN番目までのフィボナッチ数を並べたリストを返すFibHList<N extends Nat>を定義する.
type FibHListRev<N extends Nat> = {
f: HCons<Fib<N>, FibHListRev<Pred<N>>>;
t: HSingleton<Fib<_0>>;
}[IsZero<N>];
type FibHList<N extends Nat> = Reverse<FibHListRev<N>>;
let xs: FibHList<_7>; // let xs: HCons<Zero, HCons<Succ<Zero>, HCons<Succ<Zero>, HCons<Succ<Succ<Zero>>, HCons<Succ<Succ<Succ<Zero>>>, HCons<Succ<Succ<Succ<Succ<Succ<Zero>>>>>, HCons<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>, HCons<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>, HNil>>>>>>>>
この中から偶数のものだけ抜き出してみよう.
type IsEven<N extends Nat> = {
f: If<IsZero<Pred<N>>, False, Not<IsEven<Pred<N>>>>;
t: True;
}[IsZero<N>];
type FilterEven<Xs extends HList> = {
f: If<IsEven<Car<Xs>>, HCons<Car<Xs>, FilterEven<Cdr<Xs>>>, FilterEven<Cdr<Xs>>>;
t: HNil;
}[Null<Xs>];
let xs: FilterEven<FibHList<_7>>;
// let xs: HCons<Zero, HCons<Succ<Succ<Zero>>, HCons<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>, HNil>>>
_0と_2と_8だけが残った.よさそう.
本当は高階関数を渡したかったが,generic parameterを未適用のまま残して持ち回す,ということができそうにないので,諦めた.(stringの部分型に限ればmapped typeを使って簡単に定義できるのだけど.)
リストの要素をすべて足し上げるSumを定義して,0番目から9番目までのフィボナッチ数の総和を求めてみる.
type Sum<Xs extends HList> = {
f: Add<Car<Xs>, Sum<Cdr<Xs>>>;
t: _0;
}[Null<Xs>];
let a: Sum<FibHList<_9>>;
// let a: Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<
Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Su
cc<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
リストにもそろそろ飽きてきたので,Take<N extends Nat, Xs extends HList>を定義して終わりにしよう.
type Take<N extends Nat, Xs extends HList> = {
f: HCons<Car<Xs>, Take<Pred<N>, Cdr<Xs>>>;
t: HNil;
}[IsZero<N>];
type Drop<N extends Nat, Xs extends HList> = {
f: Drop<Pred<N>, Cdr<Xs>>;
t: Xs;
}[IsZero<N>];
let xs: Take<_5, FibHList<_7>>;
// let xs: let xs: HCons<Zero, HCons<Succ<Zero>, HCons<Succ<Zero>, HCons<Succ<Succ<Zero>>, HCons<Succ<Succ<Succ<Zero>>>, HNil>>>>>
let ys: Drop<_5, FibHList<_7>>;
// let ys: HCons<Succ<Succ<Succ<Succ<Succ<Zero>>>>>, HCons<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>, HCons<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Succ<Zero>>>>>>>>>>>>>, HNil>>>
株式会社HERPでは,いざという時*3に型レヴェルプログラミングでプロダクトの堅牢性を高める*4ことのできるエンジニアを募集しています.
CAMPHOR- Advent Calendar 2017,明日の担当は@tanishikingです.お楽しみに!
去年の記事もなかなかエモいのでご一緒にどうぞ.
脚注#
*1: 本当に?
*2: ちなみにここは少しごまかしていて,TypeScript 2.6系だと,「Predには任意のNは突っ込めないぞ」と怒られる.Pred<Zero>はないので,それはそう.isZeroにneverを入れておくというテクニックもあるが,これもTS 2.6だと型推論が停止せず困る.
*3: そのような時は存在するのだろうか.
*4: tscの都合でむしろ壊れることが多い.