operational (あるいは freer) と呼ばれているものの説明として，

• a) Coyoneda を使うと，kind が * -> * であるような任意の型から functor を作り出せる
  • 任意の型 f :: * -> * について Coyoneda f は Functor のインスタンスになる
• b) Free を使うと，任意の functor から monad を作り出せる
  • Functor のインスタンスである任意の型 f について Free f は Monad のインスタンスになる
• a と b を組み合わせると，適当な型 f :: * -> * から monad を作り出せて便利〜🙌

というストーリーが往々にして語られる^*1．

Free については既に多くの解説が存在するので，詳しい解説は他の記事をあたってもらうこととして，インフォーマルな説明をしておくと，以下のような気持ちを持ったデータ構造である．

• a) monad を特徴付けるのは fmap + pure + join である
• b) data Free f a = Pure a | Join (f (Free f a)) と定義されるデータ構造は，その構造内に pure と join を内包している
  • 実際，
    • Pure :: a -> Free f a
    • Join :: f (Free f a) -> Free f a
• a と b を組み合わせると，f が functor である (fmap が実装されている) ときに，Free f a は fmap, pure, join を備えているので monad と言っても過言ではない👏

補足: Join というコンストラクタは，場合によっては Free だとか Impure だとか書かれる場合があるが，これがまさに Join と名付けられていることが，私の (インフォーマルな) 理解の手助けになった．人々は親切なネーミングを心掛けてほしい．

繰り返しになるが，以上はインフォーマルな気持ちである．フォーマルな説明を求めると，monad から functor への忘却関手の左随伴だとか何とか言われて，もう勘弁してくれという気持ちになるので，お近くの圏論に詳しい方に聞いてください．

Free f a が (f が functor であるときに) monad になりそうだということはわかったので，次は Coyoneda を見てみよう．

 data Coyoneda f a = forall x. Coyoneda (x -> a) (f x)

最初に見たときは，こいつが functor になると言われても意味不明だったが，少し書き換えると理解の助けになる．a を b に，x を a に置き換えてみると，

data Coyoneda f b = forall a. Coyoneda (a -> b) (f a)

GADT で書けば^*2，

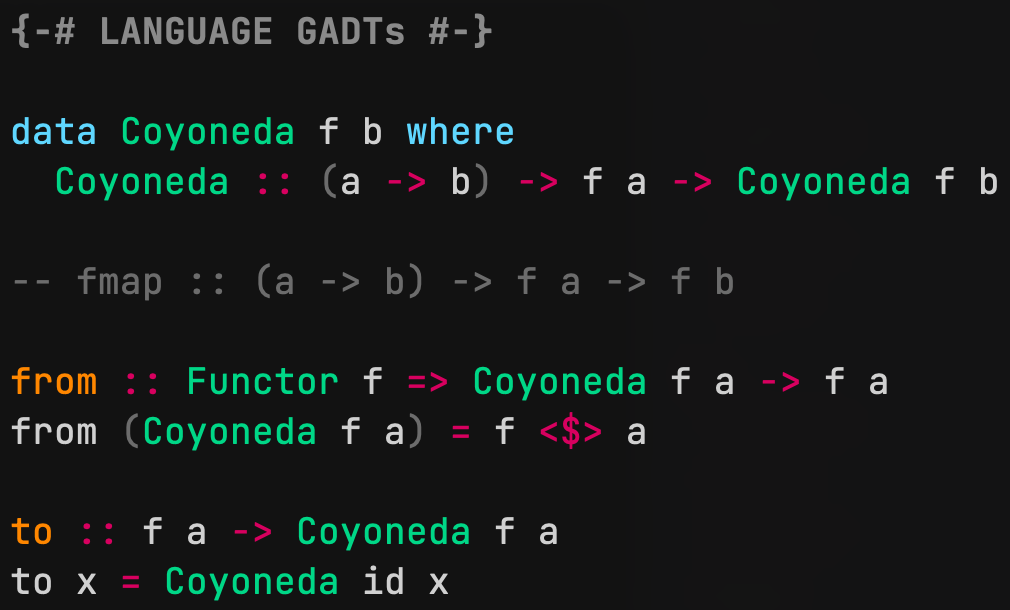
data Coyoneda f b where
    Coyoneda :: (a -> b) -> f a -> Coyoneda f b

いやいやいや，お前ほぼ fmap :: (a -> b) -> f a -> f b やんけ！！！

というわけで，Coyoneda のインフォーマルな気持ちとしては，Free が自身に monad っぽみを内包しているが故に monad として振る舞えるのと同様に，Coyoneda は自身に functor っぽみを内包しているが故に functor として振る舞えるのであった．

もちろん，データ構造それ自身が「functor っぽい」からといって，本当に functor として振る舞うのかは自明ではないが，米田の補題によって保証される，らしい．詳しくはお近くの圏論に詳しい方に聞いてください．

実際，

foo :: Functor f => Coyoneda f a -> f a
foo (Coyoneda f x) = f <$> x

bar :: f a -> Coyoneda f a
bar x = Coyoneda id x

と置くと，

foo . bar == id
bar . foo == id

と全単射が存在して安心．

free monad は monad が持つ性質をデータ構造で表現したものであることと同様に，Coyoneda は functor が持つ性質をデータ構造で表現したものであることを見た．これはインフォーマルには free functor とでも呼んでいい構造かもしれない^*3．同じようにして，free applicative functor なる構造も考えることができそうだ．

data FreeApplicative f b
    = Pure b
    | forall a. Ap (f (a -> b)) (FreeApplicative f a)

と定義すると，以下のような対応が取れる．

GADT ならこれを直接書き下して定義とすることもできる．

data FreeApplicative f b where
    Pure :: b -> FreeApplicative f b
    Ap :: f (a -> b) -> FreeApplicative f a -> FreeApplicative f b

free applicative が何の役に立つのかは知らないが，arXiv で論文を見かけた気がする．そもそも Day convolution とはなんですか．

脚注#

*1: 少なくとも2年ぐらい前に lotz 先生に聞いたときはそうだった．

*2: 実際 kan-extensions では GADT で定義されている

*3: 実際に free functor と呼ばれるものについては nLab などを参照．