一昨年のゴールデンウィークに池袋のジュンク堂を訪れた際，『形式意味論入門』という表題の本に目が止まり，数学や論理学を用いて自然言語表現の意味を形式的に考察する学問分野があることを知った^*1．また，その道具立てとして単純型付きラムダ計算が用いられていることが，なおのこと私の興味を惹いた．ラムダ計算といえば，読者の多くが計算機科学分野での応用を思い浮かべると思うが，Richard Montague^*2 が自然言語分野に応用して以来，そちらの方面でも道具立てとして用いられているようである．

この本は，Irene Heim と Angelika Kratzer による Semantics in Generative Grammar (以下 Heim and Kratzer) をベースに書かれているのだが，Heim and Kratzer で用いられる意味計算規則のうち，実質的に用いられるものはたった4つであるとし，前半で4つの意味計算規則の導入を行い，後半ではその他の自然言語現象に対して形式的な意味を与えていく，という構成になっている．また，統語論を学んだ人文学系の学生を対象読者として書かれているため．序盤では集合論やラムダ計算に関する非形式的な説明に文量が割かれている．

この記事は，私が『形式意味論入門』の内容の習得を試みる際に，自分の理解が正しいかを確かめるため，Haskell のコードとして書き下した内容を下地に書かれている．言語表現及びそれらの外延をプログラム，とりわけ Haskell のプログラムにエンコードするメリットとしては，

• 意味計算を自力で行う必要がない
• 型の整合性が GHC の型検査機によって自動的に保証される

などが挙げられるだろう．

この記事は前後編に分かれている．前編では，事前知識の導入の後，4つの意味計算規則のうち最初の2つを導入する．後編では，更なる準備の後，残る2つの意味計算規則を導入する．

§1 文の「意味」#

ここでいう「文」は平叙文のことだと思われる．たぶん元を辿ると "Satz" の訳なので，「命題」と訳してもよいのかもしれない．

合成意味論の祖である Gottlob Frege^*3 によれば，文の意味 (de: Bedeutung, en: reference) は真理値 (de: Wahrheitswerth, en: truth value) である^*4．形式意味論の分野では真理値は $0, 1$ で表されることが多いようだが，後編で導入する指標 (index) との混乱を避けるため，本記事ではそれぞれ $\text{False}, \text{True}$ と表記する．

形式意味論の研究は Richard Montague をもって嚆矢とするが，彼の思想は Donald Davidson^*5 が提唱した真理条件的意味論——すなわち，ある文の意味とは，その言語表現が真となるような状況であるとする——の流れを汲んでおり，これは現在でも形式意味論の標準的な立場となっている^*6．しかし，計算機を用いてそのような条件を得ることは難しいため，本記事では Frege に倣い，文の意味は真理値であるという立場を取ることにする．

例として，

という文の意味を考えてみよう．この主張は伝統的に正しいとされている^*7ので，この文の意味は真となるはずである．この事実を

と書く．$[\![\cdot]\!]$ は外延割当関数 (denotation assignment function) と呼ばれ，言語表現 (対象言語の項) をその意味に写す関数である．『形式意味論入門』によれば，「意味」とは

「自然言語表現」と「世界のあり方」の対応関係

として定義される^*8．また，このような定義に基づき「記号と対応する実際の存在物・概念」という意味で「意味」を捉えるとき，「外延」と呼ぶ^*9．以下この記事中では，「意味」と「外延」を区別せず用いる．

続いて，固有名詞 $\textit{Socrates}$ の意味 $[\![\textit{Socrates}]\!]$ を考えてみよう．これはもちろん古代ギリシアはアテナイの哲学者 $\text{Socrates}$ のことを指す．この事実を

と書く．左辺の外延割当関数の中にある $\textit{Socrates}$ がイタリック体になっていることに注意されたい．形式意味論では，言語を用いて言語を説明するという構造を取らざるを得ないため，説明の対象となる言語と，説明のために用いる言語とを区別しておく必要がある．これらをそれぞれ対象言語 (object language) とメタ言語 (meta language) と呼ぶ．また，混同を避けるため，対象言語はイタリック体で記述する．左辺の $\textit{Socrates}$ は単なる対象言語内の記号であり，右辺の $\text{Socrates}$ は，実在する歴史上の人物としてのソクラテスである．また，地の文で書かれているものはメタ言語である．

ところで，合成性原理 (principle of compositionality) によれば，$\textit{Socrates is mortal.}$ という文の意味は，その文中の語彙の意味

• $[\![\textit{Socrates}]\!] = \text{Socrates}$
• $[\![\textit{is}]\!] = \text{?}$
• $[\![\textit{mortal}]\!] = \text{?}$

と，それらの組み合わせ方によって，またそれらによってのみ計算されるはずである．この語彙の組み合わせ方を意味計算規則と呼ぶ．

では，語彙と意味計算規則について見ていくことにしよう．

§1のまとめ#

• 「意味」とは「自然言語表現」と「世界のあり方」の対応関係である．
• 文の意味は真理値である．
• 外延割当関数 $[\![\cdot]\!]$ は，言語表現をその意味に写す．
  • $[\![\textit{Socrates}]\!] = \text{Socrates (という人物)}$
  • $[\![\textit{Socrates is mortal.}]\!] = \text{True}$
• 文の意味は，文中の語彙の意味と，それらの組み合わせ方 (意味計算規則) によって，またそれらによってのみ計算される．

§2 意味タイプ#

例えば $\textit{Socrates}$ と $\textit{mortal}$ では，それぞれ固有名詞と形容詞であるから，それらの単語が属するカテゴリは異なることが予想される．ある単語が属する意味論上のカテゴリを意味タイプ (semantic type) と呼ぶ．混乱を生じない限り，この記事中では単に型と呼ぶ場合がある．

意味タイプは以下のように再帰的に定義される^*10．ただし $e$ は個体を表す型，$t$ は真理値を表す型，$\langle \cdot, \cdot \rangle$ は順序対である．

• a) $e$ と $t$ は意味タイプである．
• b) $\sigma$ および $\tau$ が意味タイプならば，$\langle\sigma, \tau\rangle$ も意味タイプである．
• c) 意味タイプは以上に限られる．

意味タイプを導入する目的は，項を類別することにある^*11．2つの項が，外延割当関数で移した先で同じ集合に属するならば，それらの項は同じ型をもつようにしたい．型と集合は一対一に対応する．型 $\tau$ に対応する集合を $D_\tau$ と書くことにすると，

• $D_e = \lbrace x \mid x \text{ is an individual} \rbrace$
• $D_t = \lbrace \text{False}, \text{True} \rbrace$
• $D_{\langle \sigma, \tau \rangle} = \lbrace f \mid f \text{ is a function from } D_\sigma \text{ to } D_\tau \rbrace$

となる．早い話，意味タイプとは，基底型 (ground type) $e, t$ とその上の関数型を考えたものである．読者に馴染み深い記法を用いた方が理解の助けになるであろうし，Haskell のソースコードとの対応が取れるため，この記事では $\langle \sigma, \tau\rangle$ は $\sigma \to \tau$ と表記することにする．また，この記事では，項 $x$ が型 $e$ を持つことを $x : e$ と表記する．

『形式意味論入門』から読み取るのは難しかったのだが，おそらく型は対象言語の項に付けられるものであって，メタ言語の項に付けられるものではない^*12．したがって，

という記述は妥当であり，「$\textit{Socrates}$ という語は $e$ 型を持つ」という主張になるが，

という記述は妥当でない (と思う)^*13．一方，

はメタ言語のレイヤにおける妥当な記述である．

§2のまとめ#

• 対象言語の項を類別するため，項は型 (意味タイプ) をもつ．
• 意味タイプは，個体の型 $e$ と真理値の型 $t$ およびその上の関数型 $\to$ からなる．
• 型 $\tau$ をもつ項の外延が属する集合を $D_\tau$ と書く．
  • 特に $D_e = \lbrace x \mid x \text{ is an individual} \rbrace$ (個体全部の集合)，$D_t = \lbrace \text{False}, \text{True} \rbrace$ (真理値の集合) である．

§3 様々な語彙とその意味タイプ#

§1において，文の意味は真理値であることを見た．これはすなわち，文は $t$ 型を持つことを意味する．では，文以外の項はどのような型をもつのだろうか．

3.1 $\textit{Socrates}$ の外延#

$\textit{Socrates}$ という語の意味，すなわち $[\![Socrates]\!]$ は，前述の通り，古代ギリシアの哲学者であるソクラテスのことを指している．このように，固有名詞が与えられたとき，その外延は，$D_e$ (個体全部の集合) の要素として一意に定まる．ゆえに，固有名詞は $e$ 型をもつ．

3.2 $\textit{apple} \cdot \textit{beautiful} \cdot \textit{run}$ の外延#

続いて $\textit{apple}$ という語彙の外延 $[\![apple]\!]$ を考えてみよう．ある個体 $x \in D_e$ を与えられたとき，我々は $x$ がリンゴであるかどうかを見分けることができる^*14．ゆえに，$[\![apple]\!]$ は $D_e$ の部分集合で，リンゴであるような個体だけを集めてきた集合

と言える．

あるいは，$\textit{apple}$ の外延を次のように定義してもよい．

この関数 $\chi_\text{apple}(x)$ は，定義域を $D_e$ として，引数 $x$ がリンゴであれば $\text{True}$ を，そうでなれけば $\text{False}$ を返す，いわゆる特性関数 (characteristic function) である．両者の定義間には自然な対応関係があるので，どちらを採用しても差し支えないが，Haskell で表現するに当たって特性関数の方が扱いやすいので，以後こちらの定義を用いることにする．また，

と簡単に表記する．

次に，自動詞 $\textit{run}$ の外延 $[\![run]\!]$ を考えてみよう．これも先程と同じように，すべての個体の中から，走っているもののみを選んできた部分集合

あるいは，走っている個体に対して $\text{True}$ を，それ以外に対して $\text{False}$ を割り当てる特性関数

が $\textit{run}$ の外延となる．また，$\textit{apple}$ の場合と同様に，

とも表記する．

同様に，形容詞 $\textit{beautiful}$ の外延 $[\![\textit{beautiful}]\!]$ は

である．

以上をまとめると，一般名詞・形容詞・自動詞の外延は $D_e$ から $D_t$ への関数だと思ってよさそうである．同じことだが，対象言語のレイヤでは，一般名詞・形容詞・自動詞は $e \to t$ 型をもつ．

3.3 $\textit{love}$ の外延#

他動詞 $\textit{love}$ の外延 $[\![love]\!]$ を考えてみよう．$\textit{love}$ を用いた例文として $\textit{Plato loves Socrates.}$ というものを考えてみる．

前節で自動詞 $\textit{run}$ の意味を考える際，$P_\text{run} (x) = x \text{ runs}$ という述語について，項 $x \in D_e$ を探してきてはガチャガチャと当てはめてみて，$P_\text{run} (x)$ を真にするものとそうでないものに分類したのだった．同じように $\textit{love}$ の意味を考えてみると，$P_\text{love} (x, y) = x \text{ loves } y$ という命題に対し，$x, y \in D_e$ を探してきてはガチャガチャと当てはめてみて，$P_\text{love} (x, y)$ を真にする組とそうでない組に分類してみるとよさそうだ．ここで，$\langle x, y \rangle = \langle \text{Plato}, \text{Socrates} \rangle$ という組は $P_\text{love} (x, y)$ を真にする，といった具合である．

$[\![love]\!]$ を，$P_\text{love} (x, y)$ を真にするような $D_e \times D_e$ の部分集合，つまり $D_e$ 上の二項関係^*15と捉えると，$[\![love]\!]$ は以下のように定義できる．

ところが，自然言語表現においては，$\langle x, y \rangle$ のような順序対を一語で表す機能は一般的ではなく，自然言語の構造に乗せるためには，2つの要素を1つずつ別々に渡せる方が便利である．そこで，$D_e \times D_e \to D_t$ なる関数を $D_e \to (D_e \to D_t)$ なる関数に対応付ける Schönfinkelization^*16 という操作を施す^*17．結局の所 $\textit{love}$ は $e \to e \to t$ という型を持つことになる^*18．

また，ラムダ抽象の形では以下のように書ける．

ここで $\lambda x y. x \text{ loves } y$ ではないことに注意されたい．統語構造を考えてみれば明らかだが，$\textit{love}$ と先に併合するのは主語 $y$ ではなく目的語 $x$ の方である．

§3のまとめ#

• $\textit{Socrates is mortal.}$ のような文は $t$ 型をもつ．
• $\textit{Socrates}$ のような固有名詞は $e$ 型をもつ.
• $\textit{apple}$ のような一般名詞は $e \to t$ 型をもつ．
• $\textit{run}$ のような自動詞は $e \to t$ 型をもつ．
• $\textit{beautiful}$ のような形容詞は $e \to t$ 型をもつ．
• $\textit{love}$ のような他動詞は $e \to e \to t$ 型をもつ．

§4 モデル世界意味論#

序盤で「意味」を，

「自然言語表現」と「世界のあり方」の対応関係

と定義した．しかし，この定義を愚直に採用すると，「世界」というものが曖昧である，大きすぎて取り扱いが難しい，などいった不都合が生じる^*19．そこで，意味計算に差し障りのない範囲で，箱庭のような小さな世界を考えて，この箱庭世界のあり方と自然言語表現の対応関係を考える．この「箱庭のような小さな世界」をモデルと呼ぶ．

『形式意味論入門』では $\text{Model PEANUTS}$ というモデルが想定されている．これは Charles Monroe Schulz の代表作である漫画作品『Peanuts』に由来する．以下この記事中では専ら $\text{Model PEANUTS}$ のみを考える．

$\text{Model PEANUTS}$#

$\text{Model PEANUTS}$ には，以下の8つ (のみ) の個体が存在する．それぞれに対応する言語表現と合わせて示す．

• $[\![\textit{Snoopy}]\!] = \text{Snoopy}$
• $[\![\textit{Woodstock}]\!] = \text{Woodstock}$
• $[\![\textit{Charlie}]\!] = \text{Charlie}$
• $[\![\textit{Sally}]\!] = \text{Sally}$
• $[\![\textit{Lucy}]\!] = \text{Lucy}$
• $[\![\textit{Linus}]\!] = \text{Linus}$
• $[\![\textit{Patty}]\!] = \text{Patty}$
• $[\![\textit{Schroeder}]\!] = \text{Schroeder}$

また，$\textit{boy}$ という語が存在する．この語の外延は以下の通りである．

これ以外の語彙は必要に応じて適宜導入する．

§4のまとめ#

• 「世界」は取り扱いづらいので，「モデル」と呼ばれる小さな世界を考え，その中で意味計算を行う．
• この章以降では専ら $\text{Model PEANUTS}$ についてのみ考える．

§5 対象言語を Haskell に埋め込む#

前置きが長くなったが，いよいよ意味計算を Haskell の上で行っていく．まずは準備として，対象言語を Haskell に埋め込んだ eDSL である Model 言語を導入する．

対象言語における意味タイプは，個体の型 $e$ と真理値の型 $t$ およびその上の関数型であった．$t$ 型と関数型を Haskell に落とし込むには，考えるモデルによらずそれぞれ Bool と (->) を採用すればいいが，$e$ 型はモデルによって異なってくる．そこで，$e$ 型を表す型変数 entity を取るようにしておく．

{-# LANGUAGE GADTs #-}

-- | 対象言語を Haskell に埋め込んだ eDSL
data Model entity a where
    Entity     :: entity   -> Model entity entity   -- ^ e 型の値 (個体) に相当
    TruthValue :: Bool     -> Model entity Bool     -- ^ t 型の値 (文) に相当
    Function   :: (a -> b) -> Model entity (a -> b) -- ^ a -> b 型の値に相当

また，$\text{Model PEANUTS}$ における個体を表すデータ型である PEANUTS 型を以下のように定義しておく．

data PEANUTS
    = Snoopy
    | Woodstock
    | Charlie
    | Sally
    | Lucy
    | Linus
    | Patty
    | Schroeder
    deriving (Show)

これらを組み合わせることで，$\text{Model PEANUTS}$ を Haskell に埋め込んだ Model PEANUTS 言語が得られる．ここで，対象言語内の記号 $\textit{Snoopy}$ は Entity Snoopy :: Model PEANUTS PEANUTS と表され，その外延 $[\![\textit{Snoopy}]\!]$ は Snoopy :: PEANUTS と表される．

また，外延割当関数を以下のように与える^*20．

eval :: Model entity a -> a
eval (Entity e)     = e
eval (TruthValue t) = t
eval (Function f)   = f

eval を用いると，$[\![\textit{Snoopy}]\!] = \text{Snoopy}$ という関係は eval (Entity Snoopy) = Snoopy と書くことができる．

4つの意味計算規則#

『形式意味論入門』で挙げられている4つの計算規則は以下の通りである．

• Functional Application (FA)
• Predicate Modification (PM)
• Traces and Pronouns Rule (T&P)
• Predicate Abstraction (PA)

以降の章では，これらの意味計算規則に対応する Model 言語のコンストラクタを増やすことによって，文の表現力を豊かにしていくという構成を取る．

§5のまとめ#

• Model 言語は，対象言語を Haskell に埋め込んだ eDSL である．
• 外延として Haskell の「地の文」を割り当てる．
• eval は外延割当関数であり，Model 言語の項を Haskell の項に写す．

§6 Functional Application (FA)#

§4において $\textit{boy}$ の意味を以下のように定義した．

これを Haskell に書き直すと以下のようになる．

boy :: Model PEANUTS (PEANUTS -> Bool)
boy = Function \case
    Charlie   -> True
    Linus     -> True
    Schroeder -> True
    _         -> False

さて，手始めに $\textit{Linus is a boy.}$ という文の意味計算を行いたい．まず，この文は以下のような統語構造を持つ．

ここで $\textit{is}$ と $\textit{a}$ は「語彙的に空虚」であると考える^*21．すると，合成性原理に従えば，この文の意味 $[\![\textit{Linus is a boy.}]\!]$ ——これは前述の通り真理値になる——は $[\![\textit{Linus}]\!]$ 及び $[\![\textit{boy}]\!]$ とその合成の仕方によって，またそれらによってのみ計算されるはずである．

実際のところ，どのような合成を行えばよいのだろうか．ここで第一の意味計算規則である Functional Application (FA) が導入される．$\textit{Linus} : e$ であり，かつ $\textit{boy} : e \to t$ であるから，文の意味が真理値であったことを思い出すと，直観に従って，関数適用を施した $[\![\textit{boy}]\!]([\![\textit{Linus}]\!]) \in D_t$ を意味としたいと思うのが人間の性であろう．

FA を形式的に書くと以下のようになる^*22．

$\alpha$ が，$\beta$ と $\gamma$ を娘に持つ枝分かれ節点 (branching node) で，$[\![\beta]\!]$ が $[\![\gamma]\!]$ を定義域に含む関数であるとき，$[\![\alpha]\!] = [\![\beta]\!]([\![\gamma]\!])$ である．

言い換えれば次のようになる．$\alpha$ が枝分かれ節点であり，$\beta$ および $\gamma$ を娘に持つとする．ここで $\beta$ の意味は関数であり，どのような関数かというと，定義域に $[\![\gamma]\!]$ を含んでいる．このとき，$\alpha$ の意味はどのように計算されるだろうか．その答えは，$\gamma$ の意味である項 $[\![\gamma]\!]$ に，$\beta$ の意味たる関数 $[\![\beta]\!]$ を適用した値 $[\![\beta]\!]([\![\gamma]\!])$ となる．

$\alpha$ のような節点を Model 言語に追加してみよう．left-to-right な適用と right-to-left な適用の2種類が考えられるため，それぞれに対応するコンストラクタを用意する．

data Model entity a where
    -- ...

    -- ^ left-to-right な関数適用
    FunApp_l2r :: Model entity (a -> b) -> Model entity a        -> Model entity b
    -- ^ right-to-left な関数適用
    FunApp_r2l :: Model entity a        -> Model entity (a -> b) -> Model entity b

また，eval 関数を次のように拡張する．

eval :: Model entity a -> a
-- ...
eval (FunApp_l2r l r) = eval l $ eval r
eval (FunApp_r2l l r) = eval l & eval r

$\textit{is}$ と $\textit{a}$ は語彙的に空虚であるとしたので，以下のようなユーティリティ関数 is_a を用意しておこう．

is_a :: Model entity a -> Model entity (a -> b) -> Model entity b
is_a = FunApp_r2l

is_a 関数を使えば，文 $\textit{Linus is a boy.}$ は以下のように Haskell に埋め込むことができる．

sentence :: Model PEANUTS Bool
sentence = Entity Linus `is_a` boy

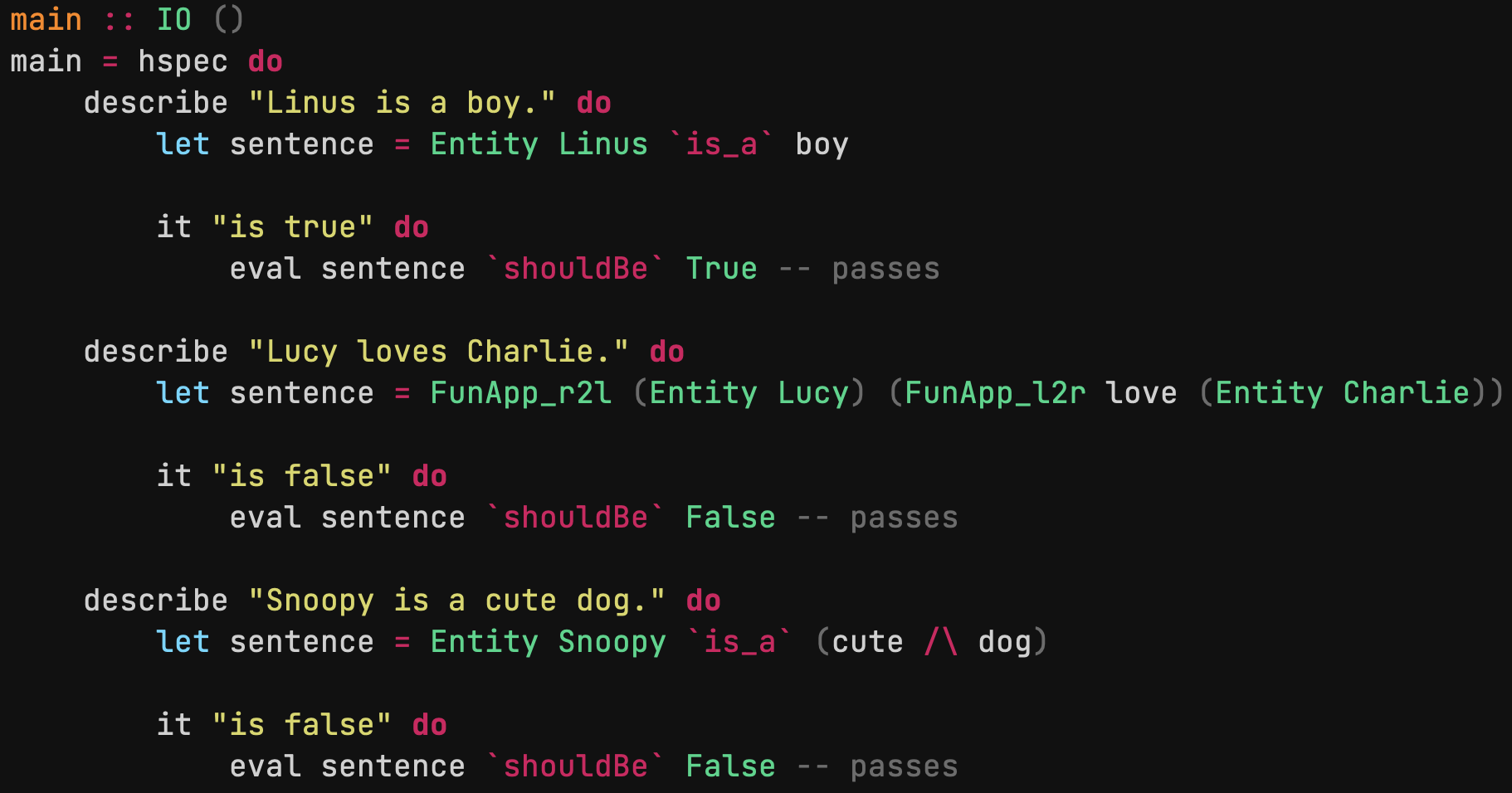
さて，それでは実際に意味計算を行ってみよう．

main :: IO ()
main = hspec do
    describe "Linus is a boy." do
        let sentence = Entity Linus `is_a` boy

        it "is true" do
            eval sentence `shouldBe` True -- passes

同じように，$\textit{Lucy loves Charlie}$ の外延を計算してみる．統語構造は以下のような形である．

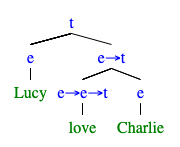
$\textit{Model PEANUTS}$ において $\textit{love}$ の意味を以下のように定義する．

love :: Model PEANUTS (PEANUTS -> PEANUTS -> Bool)
love = Function $ \object subject -> case (subject, object) of
  (Lucy , Schroeder) -> True
  (Sally, Linus    ) -> True
  (Patty, Charlie  ) -> True
  _                  -> False

この上で意味計算を行うと以下のようになる．

main :: IO ()
main = hspec do
    describe "Lucy loves Charlie." do
        let sentence = FunApp_r2l (Entity Lucy) (FunApp_l2r love (Entity Charlie))

        it "is false" do
            eval sentence `shouldBe` False -- passes

§6のまとめ#

• FA という意味計算規則が導入された．
  • $\alpha$ が，$\beta$ と $\gamma$ を娘に持つ枝分かれ節点で，$[\![\beta]\!]$ が $[\![\gamma]\!]$ を定義域に含む関数であるとき，$[\![\alpha]\!] = [\![\beta]\!]([\![\gamma]\!])$ である．

§7 Predicate Modification (PM)#

$\textit{Snoopy is a cute dog.}$ という文の意味を計算したい．統語構造は次のとおりである．

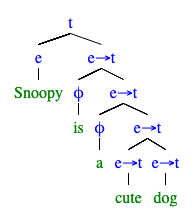
ここで，$\textit{cute}$ と $\textit{dog}$ を娘に持つ節点に注目したい．$cute : e \to t$ であり，かつ $dog : e \to t$ なので，FA では型が合わない．このような節点の意味を計算するための規則として Predicate Modification (PM) を導入する^*23．

$\alpha$ が枝分かれ節点で，$\beta, \gamma$ がともに $\alpha$ の娘であり，$[\![\beta]\!] \in D _ {e \to t}$ かつ $[\![\gamma]\!] \in D_{e \to t}$ であるとき，$[\![\alpha]\!] = \lambda x \in D_e. [\![\beta]\!](x) \land [\![\gamma]\!](x)$ である．

$x \in D _ e$ に関する2つの述語 $[\![\beta]\!] = \lambda x.P(x)$ と $[\![\gamma]\!] = \lambda x.Q(x)$ が与えられたならば，それらの論理積を取った新しい述語 $\lambda x. P(x) \land Q(x)$ として取り扱おう，というアイディアである．

PM を Model 言語に追加してみよう

data Model entity a where
    -- ...
    PredicateModification
        :: Model entity (entity -> Bool) -- λx.P(x)
        -> Model entity (entity -> Bool) -- λx.Q(x)
        -> Model entity (entity -> Bool) -- α = λx.P(x)∧Q(x)

eval :: Model entity a -> a
-- ...
eval (PredicateModification p q) = \x -> eval p x && eval q x

PM と FA を用いて $\textit{Snoopy is a cute dog.}$ の意味を計算すると，$(\lambda x. [\![\textit{cute}]\!](x) \land [\![\textit{dog}]\!](x))([\![Snoopy]\!])$，すなわち $[\![\textit{cute}]\!](\text{Snoopy}) \land [\![\textit{dog}]\!](\text{Snoopy})$ となる．

$\text{Model PEANUTS}$ において $\textit{cute}$ と $\textit{dog}$ の意味を次のように定義する．

cute :: Model PEANUTS (PEANUTS -> Bool)
cute = Function \case
    Lucy  -> True
    Patty -> True
    Sally -> True
    _     -> False

dog :: Model PEANUTS (PEANUTS -> Bool)
dog = Function \case
    Snoopy -> True
    _      -> False

この上で意味計算を行ってみよう．

-- | 'PredicateModification' を表すヘルパー関数
(/\) :: Model entity (entity -> Bool) -> Model entity (entity -> Bool) -> Model entity (entity -> Bool)
(/\) = PredicateModification

main :: IO ()
main = do
    describe "Snoopy is a cute dog." do
        let sentence = Entity Snoopy `is_a` (cute /\ dog)

        it "is false" do
            eval sentence `shouldBe` False -- passes

Snoopy が cute であるかどうかについては議論が分かれるところだと思うが，少なくとも $\text{Model PEANUTS}$ における $\textit{cute}$ の定義に照らし合わせれば，$[\![\textit{Snoopy is a cute dog.}]\!]$ は偽ということになる．

§7のまとめ#

• PM という意味計算規則が導入された．
  • $\alpha$ が枝分かれ節点で，$\beta, \gamma$ がともに $\alpha$ の娘であり，$[\![\beta]\!] \in D_{e \to t}$ かつ $[\![\gamma]\!] \in D_{e \to t}$ であるとき，$[\![\alpha]\!] = \lambda x \in D_e. [\![\beta]\!](x) \land [\![\gamma]\!](x)$ である．

後編に向けて#

続く第3・第4の意味計算規則である "Traces and Pronouns Rule (T&P)" および "Predicate Abstraction (PA)" を取り扱うためには，変項割当 (variable assignment) という概念を導入せねばならず，Model 言語を大きく拡張しなければならない．変項割当は，$\textit{She}_4$ のような，指標 (index) の付いた代名詞などを扱うための仕組みである．$4$ という指標に対応する個体が何であるかは文脈によって規定されるのだが，私にはこれは計算的効果 (computational effect) に見える．後編では，変項割当を扱うための仕組みを用意したのち，残りの意味計算規則を見ていくこととしよう．

コード全文#

#!/usr/bin/env stack
-- stack --install-ghc runghc --package hspec

{-# LANGUAGE BlockArguments #-}
{-# LANGUAGE GADTs #-}
{-# LANGUAGE LambdaCase #-}

import Data.Function ((&))
import Test.Hspec (describe, hspec, it, shouldBe)

-- | 対象言語を Haskell に埋め込んだ eDSL
data Model entity a where
    Entity     :: entity -> Model entity entity   -- ^ e 型の値に相当
    TruthValue :: Bool -> Model entity Bool     -- ^ t 型の値 (文) に相当
    Function   :: (a -> b) -> Model entity (a -> b) -- ^ a -> b 型の値に相当

    FunApp_l2r :: Model entity (a -> b) -> Model entity a -> Model entity b
    FunApp_r2l :: Model entity a -> Model entity (a -> b) -> Model entity b

    PredicateModification
        :: Model entity (entity -> Bool) -- ^ λx.P(x)
        -> Model entity (entity -> Bool) -- ^ λx.Q(x)
        -> Model entity (entity -> Bool) -- ^ λx.P(x)∧Q(x)

-- | 外延割当関数
eval :: Model entity a -> a
eval (Entity e)                  = e
eval (TruthValue t)              = t
eval (Function f)                = f
eval (FunApp_l2r l r)            = eval l $ eval r
eval (FunApp_r2l l r)            = eval l & eval r
eval (PredicateModification p q) = \x -> eval p x && eval q x

data PEANUTS
    = Snoopy
    | Woodstock
    | Charlie
    | Sally
    | Lucy
    | Linus
    | Patty
    | Schroeder
    deriving (Show)

boy :: Model PEANUTS (PEANUTS -> Bool)
boy = Function \case
    Charlie   -> True
    Linus     -> True
    Schroeder -> True
    _         -> False

cute :: Model PEANUTS (PEANUTS -> Bool)
cute = Function \case
    Lucy  -> True
    Patty -> True
    Sally -> True
    _     -> False

dog :: Model PEANUTS (PEANUTS -> Bool)
dog = Function \case
    Snoopy -> True
    _      -> False

is_a :: Model entity a -> Model entity (a -> b) -> Model entity b
is_a = FunApp_r2l

(/\) :: Model entity (entity -> Bool) -> Model entity (entity -> Bool) -> Model entity (entity -> Bool)
(/\) = PredicateModification

main :: IO ()
main = hspec do
    describe "Linus is a boy." do
        let sentence = Entity Linus `is_a` boy

        it "is true" do
            eval sentence `shouldBe` True -- passes

    describe "Lucy loves Charlie." do
        let sentence = FunApp_r2l (Entity Lucy) (FunApp_l2r love (Entity Charlie))

        it "is false" do
            eval sentence `shouldBe` False -- passes

    describe "Snoopy is a cute dog." do
        let sentence = Entity Snoopy `is_a` (cute /\ dog)

        it "is false" do
            eval sentence `shouldBe` False -- passes

脚注#

*1: ちなみに，意味論を研究する研究室に所属する友人に聞いたところ，形式意味論の入門に当たっては，Elements of Formal Semantics がおすすめだそうである．

*2: アメリカの数学者・哲学者．博士課程時代には Banach-Tarski のパラドクスで知られる Alfred Tarski の門下で公理的集合論を研究．その後，Tarski より学んだ数理論理学におけるモデル意味論を自然言語の意味論に応用する研究に着手し，今日の形式意味論の草分け的存在となった．

*3: ドイツの哲学者・論理学者・数学者．アリストテレス以来2,000年以上に渡って用いられていた論理学を再定義し，形式的な記号を用いて議論することを可能にした．今日の数理論理学の祖として知られる．

*4: ちなみに，文の意義 (de: Sinn, en: sense) は，その文が真ないし偽と規定される仕方である．

*5: アメリカ合衆国の哲学者．彼の思想は哲学の多くの分野，とりわけ行為論・心の哲学・言語哲学に大きな影響を与えた．

*6: http://www.is.ocha.ac.jp/~bekki/project.html

*7: ソクラテスは人間であり，任意の人間は死ぬので．全称肯定判断 (A) として知られている．

*8: 『形式意味論入門』 p.3

*9: 『形式意味論入門』 p.11

*10: Heim and Kratzer §2.3

*11: と少なくとも私は読み取った．不文律として「ある項はちょうどひとつの型をもつ」というものがあると思うのだが，classification と捉えるとこれがうまくハマる．

*12: 少なくとも Heim and Kratzer では厳密に区別されていない．

*13: 前述の通り，型と集合は一対一に対応するため，そこまで厳密に区別する必要性も無いのかもしれないが．

*14: できると思ってほしい．

*15: Nicht: »Das komplexe Zeichen ›aRb‹ sagt, dass a in der Beziehung R zu b steht«, sondern: Dass »a« in einer gewissen Beziehung zu »b« steht, sagt, dass aRb. (Tractatus 3.1432)

*16: ロシアの論理学者・数学者である Moses Schönfinkel に由来する．

*17: 我々が "currying" として知っている操作である．

*18: $\to$ は右結合であると約束する．

*19: 『形式意味論入門』p. 31 では，この定義のもとで $\textit{student}$ の外延を考えるには，「実際にこの世界中ですべての「学生」を知っていないと，この外延は定義できないことになる．」と述べられている．

*20: これは一見自明に見えるが，必ずしもそうではない．Heim and Kratzer §3.1 において，"If $\alpha$ is a terminal node, $[\![\alpha]\!]$ is specified in the lexicon." という規則が与えられている．

*21: この取り扱いが妥当なのかはちょっとわかっていない．導入部分では捨象していい程度の問題なのだろうか．

*22: Heim and Kratzer §3.

*23: Heim and Kratzer §4.3.1